Method & Apparatus for the Exploitation of Piezolectricity in Carbon Based Life Forms by Timothy Winey

BACKGROUND OF THE INVENTION

Piezoelectricity is the ability of certain crystals to produce a Voltage when Subjected to mechanical stress. The word is derived from the Greek piezein, which means to squeeze or press. The effect is reversible; piezoelectric crystals, Subject to an externally applied Voltage, can change shape by a small amount. The effect is of the order of nanometres, but nevertheless finds useful applications such as the production and detection of sound, generation of high Voltages, electronic frequency generation, and ultrafine focusing of optical assemblies.

In a piezoelectric crystal, the positive and negative electrical charges are separated, but symmetrically distributed, so that the crystal overall is electrically neutral. When a stress is applied, this symmetry is disturbed, and the charge asymmetry generates a Voltage. A 1 cm cube of quartz, With 500 lb (2 kN) of correctly applied pressure upon it, can produce 12,500 V ofelectricity. Piezoelectric materials also

show the opposite effect, called converse piezoelectricity, where application of an electrical field creates mechanical stress (distortion) in the crystal. Because the charges inside the crystal are separated, the applied voltage affects different points within the crystal differently, resulting in the distortion. The bending forces generated by converse piezoelectricity are extremely high, of the order of tens of millions of

pounds (tens of meganewtons), and usually cannot be constrained. The only reason the force is usually not noticed is because it causes a displacement of the order of one billionth of an inch (a few nanometres).

A related property known as pyroelectricity, the ability of certain mineral crystals to generate electrical charge when heated, was known of as early as the 18th century, and was named by David Brewster in 1824. In 1880, the brothers Pierre Curie and Jacques Curie predicted

and demonstrated piezoelectricity using tinfoil, glue, wire, magnets, and a jeweler’s saw. They showed that crystals of tourmaline, quartz, topaz, cane Sugar, and Rochelle Salt (sodium potassium tartrate tetrahydrate) generate electrical polarization from mechanical stress. Quartz and Rochelle salt exhibited the most piezoelectricity. Twenty natural crystal classes exhibit direct piezoelectricity. Converse piezo

electricity was mathematically deduced from fundamental thermodynamic principles by Lippmann in 1881. The Curies immediately confirmed the existence of the “converse effect,” and went on to obtain quantitative proof of the complete reversibility of electro-elasto-mechanical deformations in piezoelectric crystals.

The polymer polyvinylidene fluoride, (-CH2CF2-)n, exhibits piezoelectricity several times larger than quartz. Bone exhibits some piezoelectric properties: it has Nov. 8, 2007 been hypothesized that this is part of the mechanism of bone remodelling in response to stress.

Piezoelectric crystals are used in numerous ways:

Direct piezoelectricity of some substances like quartZ, as mentioned above, can generate thousands of volts (known as high-voltage differentials).

A piezoelectric transformer is a type of AC voltage multiplier. Unlike a conventional transformer, which uses magnetic coupling between input and output, the piezoelectric transformer uses acoustic coupling. An input Voltage is applied across a short length of a bar of piezoceramic material Such as PZT, creating an alternating stress in the bar by the inverse piezoelectric effect and causing the whole bar

to vibrate. The vibration frequency is chosen to be the resonant frequency of the block, typically in the 100 kilo hertz to 1 megahertz range. A higher output voltage is then generated across another section of the bar by the piezoelectric effect. Step-up ratios of more than 1000:1 have been demonstrated. An extra feature of this transformer is that, by operating it above its resonant frequency, it can be made to appear as an inductive load, which is useful in circuits that require a controlled Soft start. 

In this application, the use of the terms clubhead or head, unless stipulated as being part of a particular club type, herein are used to refer generically to the striking portion of any golf club whereas the term putterhead refers to a special case of clubhead used for putting. Similarly, the terms shaft or club shaft, are used generically to refer to the elongated tubular sections of all golf clubs to which the heads attach whereas putter shaft refers specifically to shafts used for putters only. In addition, the term “golf shot” refers generically to any striking of a golf ball with any club whereas putts are to be construed as a special kind of golf shot executed by special clubs known by those skilled in the art as putters.

Also, the term graphic will refer to images within the main body of this application whereas the term figure will refer to the drawings section of this application except when referring specifically to the mathematical category of geometric figures. To eliminate any possible confusion, the inventor has truncated the word figure to “Fig.” When referring to any patent drawings. 

Harmonics are often also referred to as overtones, but the precise definition of overtone for the purpose of this application, refers to a particular partial in the timbre. For example, an instrument could contain 3 overtones—say . . . harmonics 1, 2, 5 and 8. Harmonic 1 is the fundamental so this doesn’t count. Harmonic 2 is overtone 1, harmonic 5 is overtone 2, and 8 is the third overtone.

2=overtone 1.

Harmonic 3=overtone 2.

Harmonic 4 =overtone 3 and so on.

In order to demonstrate how the inventor exploits the use of phi ratios and related recursive or self-similar phenomena that may not, in and of themselves, result in exact mathematical phi, but rather, represent the minimum entropy of a fractal system, striking the balance between maximum order and flexible variation, that may contribute to an improved putting technique via enhanced feedback and how they, in turn, feed back onto improved putting technique based partially on holographic theory, he directs the examiners attention to an overview of quantum physical and fractal phenomena as they relate to, and connect with, the ideas of self-organizing structures, learning theory, piezoelectric signaling and resultant biological phenomena to the extent they inform this invention.

Examples of devices that exploit the ability of the body to entrain, induce and promote brainwave coherence include:

1. Patrick Flanagan’s Neurophone (U.S. Pat. No. 3.393.279). Flanagan also conducted experiments involving phi geometries and their effects on muscle strength. He played Pink Noise using various geometric shapes as resonators; a model of the Great Pyramid, models of the King’s Chamber; Dodecahedrons and the like, to modify the Pink Noise. He then had experts in applied kinesiology test the muscles strength of people listening to the same sounds resonated through said shapes. The results were unanimous, the Pyramid shapes based on the Golden Ratio made people very strong. Cubes made people very weak. 

2. European patent (number 0351357) filed in 1989 by the chemical giant Ciba-Geigy for a way to cultivate original forms of plants and animals using simple electrostatic fields termed The Ciba-Geigy Effect. The patent is simply called “Improved Cultivation Technique’, described as “A novel method is described, which, on the basis of the short-term application of electrostatic fields, results in lasting beneficial and desirable properties in fish, which are otherwise achievable only with a substantial additional effort, if at all. As a result of the simplicity of the measures constituting the method according to the invention and the significant results, the culture of fish, particularly of edible fish but also of ornamental fish, is genuinely revolutionized.

3. The Austrian physicist Viktor Schauberger’s work will be essential in shedding light on Subtle energy phenomena and their reflection in self-organizing structures and related phenomena.

4. Similar to the Flanagan Neurophone, which uses electrical current, in 1975, Robert Monroe was issued an original patent (number not known) in the field of altering brain states through sound. His compelling research became the foundation for a noninvasive and easy-to-use “audio guidance’ technology known as Hemi-Sync, which has been proven to produce identifiable, beneficial effects, including

enhancing alertness, inducing sleep, and evoking expanded states of consciousness. 

5. The HeartTuner is a multi-purpose measurement and biofeedback system for therapists, health professionals, researchers, and individual use. In addition to harmonic analysis (power spectra) of Heart (ECG/HRV), Brain (EEG), the HeartTuner directly measures Internal Cardiac Coherence (“ICC). These so-called coherences are based on phi geometry and as any cardiologist will tell you, are strongly

predictive of mortality in addition to reflecting mental and physical states.

In nature, we find geometric patterns, designs and structures from the most minuscule particles, to expressions of life discernible by human eyes, to the greater cosmos. These inevitably follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances. They are also symbolic of the underlying meta physical principle of the inseparable relationship of the part

to the whole. It is this principle of oneness underlying all geometry that permeates the architecture of all form in its myriad diversity.

Life itself as we know it is inextricably interwoven with geometric forms, from the angles of atomic bonds in the molecules of the amino acids, to the helical spirals of DNA, to the spherical prototype of the cell, to the first few cells of an organism which assume vesical, tetrahedral, and star (double) tetrahedral forms prior to the diversification of tissues for different physiological functions. Our human bodies on this planet all developed with a common geometric progression from one to two to four to eight primal cells

and beyond.

 Golden ratio of segments in 5-pointed star (pentagram) were considered sacred to Plato & Pythagoras in their mystery Schools. Note that each larger (or Smaller) section is related by the phi ratio, so that a power series of the golden ratio raised to successively higher (or lower) powers is automatically generated: phi, phi^2, phi^3, phil^4, phi^5, etc. 

Phi=apothem to bisected base ratio in the Great Pyramid of Giza

Fibonacci ratios appear in the ratio of the number of spiral arms in daisies, in the chronology of rabbit populations, in the sequence of leaf patterns as they twist around a branch, and a myriad of places in nature where self generating patterns are in effect. The sequence is the rational progression towards the irrational number embodied in the quintessential golden ratio. 

This spiral generated by a recursive nest of Golden Triangles (triangles with relative side lengths of 1, phi and phi) is the classic shape of the Chambered Nautilus shell. The creature building this shell uses the same proportions for each expanded chamber that is added; growth follows a law, which is everywhere, the same. 

Toroids result when rotating a circle about a line tangent to it creates a torus, which is similar to a donut shape where the center exactly touches all the “rotated circles.” The surface of the torus can be covered with 7 distinct areas, all of which touch each other; an example of the classic “map problem’ where one tries to find a map where the least number of unique colors are needed. In this 3-dimensional

case, 7 colors are needed, meaning that the torus has a high degree of “communication” across its Surface.

The progression from point (0-dimensional) to line (1-dimensional) to plane (2-dimensional) to space (3-dimensional) and beyond leads us to the question if mapping from higher order dimensions to lower ones loses vital information (as wecan readily observe with optical illusions resulting from third to second dimensional mapping), then perhaps our“fixation’ with a 3-dimensional space introduce

crucial distortions in our view of reality that a higher dimensional perspective would not lead us to.

The 3/4/5, 5/12/13 and 7/24/25 triangles are examples of right triangles whose sides are whole numbers. The 3/4/5 triangle is contained within the so-called “King’s Chamber of the Great Pyramid, along with the 2/3/roots and 5/rootS/2rootS triangles, utilizing the various diagonals and sides.

The 5 Platonic solids (Tetrahedron, Cube or (Hexahedron), Octahedron, Dodecahedron & Icosahedron) are ideal, primal models of crystal patterns that occur through out the world of minerals in countless variations. These are the only five regular polyhedra, that is, the only five solids made from the same equilateral, equiangular polygons. To the Greeks, these solids symbolized fire, earth, air, spirit (or

ether) and water respectively. The cube and octahedron are duals, meaning that one can be created by connecting the midpoints of the faces of the other. The icosahedron and dodecahedron are also duals of each other, and three mutually perpendicular, mutually bisecting golden rectangles can be drawn connecting their vertices and midpoints, respectively. The tetrahedron is a dual to itself.

Phyllotaxis is the study of symmetrical patterns or arrangements. This is a naturally occurring phenomenon. Usually the patterns have arcs, spirals or whorls. Some phyllotactic patterns have multiple spirals or arcs on the Surface of an object called parastichies. The spirals have

their origin at the center C ofthe surface and travel outward, other spirals originate to fill in the gaps left by the inner spirals. Frequently, the spiral-patterned arrangements can be viewed as radiating outward in both the clockwise and counterclockwise directions. These types of patterns have visibly opposed parastichy pairs where the number of spirals or arcs at a distance from the center of the object radiating

in the clockwise direction and the number of spirals or arcs radiating in the counterclockwise direction. Further, the angle between two consecutive spirals or arcs at their center is called the divergence angle. 

The Fibonnaci-type of integer sequences, where every term is a sum of the previous two terms, appear in several phyllotactic patterns that occur in nature. The parastichy pairs, both m and n, of a pattern increase in number from the center outward by a Fibonnaci-type series. Also, the divergence angle d of the pattern can be calculated from the series.

Indelibly etched on the walls of temple of the Osirion at Abydos, Egypt, the Flower of Life contains a vast Akashic system of information, including templates for the five Platonic Solids.

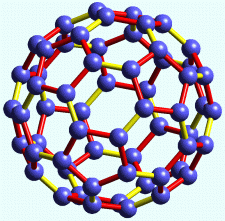
The inventor wishes to exploit the fractal geometries of so-called “fullerenes’ to include both “simple” and “perfect fullerene shapes insofar as they also have been shown to exhibit unique vibrational and stiffening properties. The inventor will exploit fullerene geometries at the molecular or nano-scale and at the macro scale to be employed in golf clubs, golf shafts, and other items. The determination of what constitutes a fullerene mathematically as well as differentiates general from perfect fullerenes, is given below.

Among all elements, C is the basis of entire life. The whole branch of chemistry—the organic chemistry—is devoted to the study of C

C bonds and different molecules originating from them. Carbon is the only 4-valent element able to produce long homoatomic stable chains or different 4-regular nets. The other 4-valent candidate for this could be only Si, with its reach chemistry beginning to develop. After diamond and graphite—the hexagonal plane hollow shell, in 1985 was first synthesized by H. W. Kroto, R. F. Curl and R.

E. Smalley the spherical closed pentagonal/hexagonal homoatomic shell: the fullerene C60. Except from this, it possesses someanother remarkable properties: the rotational symmetry of order 5, from the geometrical reasons (according to Barlow “crystallographic restriction theorem) forbidden in crystallographic space or plane symmetry groups, and highest possible icosahedral point-group symmetry.

After C60, different fullerenes (e.g. C70. C76.fc78. C82. C84 etc.) are synthesized, opening also a new field for research of different potentially possible fullerene structures from the geometry, graph theory or topology point of view.

From the tetravalence of C result four possible vertex situations, that could be denoted as 31, 22, 211 and 1111 (Graphic 1a). The situation 31 could be obtained by adding two C atoms between any two others connected by a single bond, and situation 22 by adding a C atom between any two others connected by a double bond Graphic 1b. Therefore, we could restrict our consideration to the remaining two non-trivial cases: 211 and 1111. Working in opposite sense, we could always delete 31 or 22 vertices, and obtain a reduced 4-regular graph, where in each vertex occurs at most one double bond (digon), that could be denoted by colored (bold) edge (Graphic la). First, we could consider all 4-regular graphs on a sphere, from which non-trivial in the sense of derivation are only reduced ones. In the knot

theory, 4-regular graphs on a sphere with all vertices of the type 1111 are known as “basic polyhedra’1,2,3,4), and that with at least one vertex with a digon as ‘generating knots or links’4). From the chemical reasons, the vertices of the type 1111 are only theoretically acceptable. If all the vertices of such 4-regular graph are of the type 211. Such graph we will be called a general fullerene. Every general fullerene could be derived from a basic polyhedron by “vertex bifurcation’, this means, by replacing its vertices by digons, where for

their position wehave always two possibilities (Graphic 1c). To every general fullerene corresponds (up to isomorphism) an edge-colored 3-regular graph (with bold edges denoting digons).

This way, we have two complementary ways for the derivation of general fullerenes: vertex bifurcation method applied to basic polyhedra, or edge-coloring method applied to 3-regular graphs, where in each vertex there is exactly one colored edge. For every general fullerene we could define its geometrical structure (i.e. the positions of C atoms) described by a non-colored 3-regular graph, and its chemical structure (i.e. positions of C atoms and their double bonds) described by the corresponding edge-colored 3-regular graph. In the same sense, for every general fullerene we could distinguish two possible symmetry groups: a symmetry group G corresponding to the geometrical structure and its subgroup G’ corresponding to the chemical structure. In the same sense, we will distinguish geometrical and chemical isomers.